Haldane's Dilemma

Haldane's Dilemma

by Laurence D Smart B.Sc.Agr., Dip.Ed., Grad.Dip.Ed

[Free to print and distribute. Copy must be in full.]

For evolution to occur, 'old' genes must be replaced by 'new', more advanced genes. This replacement has to occur in the entire population of a species if it is to evolve into another species.

Individuals with new, rare genes have to completely replace all the members of the existing population for the new genes to take over. This replacement depends on the reproductive capacity of the species, and how well the new individuals survive.

Early this century, the advent of the science of population genetics was seen as the final corroborating proof of evolution. However, in the 1950's, an evolutionary geneticist by the name of John Haldane used population genetics to calculate the maximum rate that genetic change could take place. He took into account the costs that evolution places on a species, and the results of his calculations produced a dilemma for evolutionists that few people know about.

The Calculation

Let's follow Haldane's logic and see if it is theoretically possible for an ape to evolve into a human in 10 million years. The calculation below takes into account the costs that the species has to forego in its evolution when the 'less fit' die.

Like Haldane, the calculation uses average figures for the costs, and perfect conditions for evolution, so that the results are the most optimistic for the evolutionist.

Note: In genetics, a trait is a characteristic such as, longer wings, whiter fur, and shorter ears.

Data:

Population size = 100,000

Length of a generation = 20 years

Status for the new trait = higher survival rate than the old trait

New trait generation method = mutation

Mode of action of mutation = alteration of one DNA nucleotide in the chromosomes

Amount of genetic material = 7x10⁹ nucleotide sites in the DNA (typical of a mammal)

Length of evolution = 10,000,000 years (10 million years)

Type of evolution = perfect, uninterrupted & continuous for the whole time

Contra-evolution factors = not considered

Analysis:

QUESTION 1: What is the average Cost of Substitution in populations today? (The Cost of Substitution is the ratio of survivors with new traits to those with the old trait that are unfit and die.)

Answer: 30:1 (see ReMine p:216)

QUESTION 2: If a higher vertebrate is to maintain its population size, what is its Reproductive Excess - the number of excess individuals that it can afford to lose?

Answer: 10% (see ReMine p:216)

QUESTION 3: How long would it take for one nucleotide to completely replace an old one?

Answer: 300 generations (ie 30÷10% ie Cost of Substitution/Reproductive Excess)

QUESTION 4: How many nucleotides could be replaced in the 10 million years of our example?

Answer: 1,667 (ie 10,000,000yrs÷20yrs x 300 generations)

QUESTION 5: Therefore, how much of the apes genetic material would be replaced in the 10 million years of the example?

Answer: 0.00002% (ie 1667÷7x10⁹x100)

Explanation: 1,667 nucleotides is 0.00002%, if the apes had the typical amount of genetic material.

QUESTION 6: Is this enough change to evolve a simian into a sapien, an ape into a human?

Answer: No

QUESTION 7: How long would it take to evolve an ape into a human?

Answer: 500 billion yrs for just 1% change (ie 10,000,000 yrs ÷ 0.00002%)

Explanation: At this rate of replacement it would take 500 billion years for just 1% of the genes to be replaced. One percent change wouldn't even change an ape into a new ape species.

Problem:

This scenario is based on perfect conditions for evolution. It does not take into account the factors that work against evolution.

QUESTION 8: What factors work against perfect evolution?

Answer: To itemize just a few:- *

(1) Good (beneficial) mutations are always rare - not even one every generation.

(2) The harmful effects of detrimental mutations can devastate a population.

(3) The period of time that the population is without change (called stasis) must be included. Gould estimates that the fossil record shows that a typical species spends 90% of its time in stasis. (See New Scientist, April 15, 1982 p:137)

(4) Inbreeding of the survivors would result in the loss of many useful traits.

(5) Because most traits are the result of the action of many genes, and not just one nucleotide (as in our example), the introduction of a trait may take many mutations.

(6) Each nucleotide can act in more than one gene. So, any changes in nucleotides may produce beneficial effects in one gene, but detrimental effects in others.

(* See ReMine footnote #7 - p:210)

QUESTION 9: Does gene dominance affect the Cost of Substitution?

Answer: Yes.

Explanation: Recessive genes are more costly than dominant ones because they actually select against themselves. The table below shows that 100,011 entire populations must be eliminated during the replacement of a single recessive gene if it begins in a single individual in a population of 50,000. Recessive genes greatly slow down the rate of evolution. (see ReMine p:216)

Starting Occurrence of Gene	Cost of Dominant Gene	Cost of Recessive Gene
500,000	14	1,000,013
50,000	12	100,011
5,000	9	10,008
500	7	1,006

QUESTION 10: How long would it take to change 10% of this genetic material?

Answer: 5,000 billion yrs (500 bil. yrs x 10)

QUESTION 11: How long would it take if 90% of the time was in stasis?

Answer: 50,000 billion yrs (5,000 bil. yrs x 10)

BUT.... (1) Apes are said to have evolved into humans in 5 million years

BUT.... (2) The earth is said to be only 5 billion years old

BUT.... (3) The Big Bang is said to have occurred 20 billion years ago

The Conclusion

Haldane has shown mathematically that there is a flaw in the theory of evolution. Using average data and perfect conditions for evolution, he has shown that there has not been enough time for evolution to have occurred - not even for human evolution.

Evolutionists' Response

Evolutionists have tried to deny, overlook, talk around, explain away, and discredit Haldane's work over the past 40 years, but they have not succeeded.

Generally, evolutionists have turned a blind-eye to Haldane's work. Most textbooks ignore it.

"A few years later [following Gould's proposal of his Punctuated Equilibrium theory], punctuationists made a subtle attempt to 'decouple' genetic evolution from morphological evolution, as though the two are not closely related. Possibly a geneticist had made them aware of Haldane's Dilemma, and the decoupling was suggested as a way to avoid amplifying the problem. If that is true, punctuationists have not actually said so. Haldane's Dilemma has remained the trade secret of evolutionary geneticists." (ReMine footnote #6 - p:210) emphasis mine

Few geneticists acknowledge it.

"Haldane's dilemma lay in the fact that the cost of evolution appeared to be so extremely high that to bring the cost within reasonable bounds, it appeared that the rate of evolution had to be inordinately low." (D.J. Merrell "Ecological Genetics", University of Minnesota Press, 1981 p:189) emphasis mine

Some attack it.

The Appendix at the end shows a typical example of such an attack.

References to Haldane's Work

J.B.S. Haldane, "The Cost of Natural Selection", Journal of Genetics, Vol. 55, 1957 p:511-524

J.B.S. Haldane, "More Precise Expressions for the Cost of Natural Selection", Journal of Genetics, Vol. 57, No. 2&3, 1961 p:351-360

J.B.S. Haldane, in "On Being the Right Size and Other Essays", (John Maynard-Smith ed.), Oxford University Press: New York, 1985

SOURCE: W.J. ReMine "The Biotic Message", St Paul Science: Saint Paul (USA), 1993 p:208-236

APPENDIX

Here is an example of a typical attack on Haldane's work.

The Attack: "..... Haldane's calculations pertain to large populations, while rapid evolutionary changes happen most frequently in small populations." E. Mayr "The Growth of Biological Thought: Diversity, Evolution and Inheritance", The Belknap Press of Harvard University Press, 1982 p:594

The Defence: "In small populations, harmful genes can rapidly replace beneficial genes, simply by chance. This is a common result of genetic drift and inbreeding in small populations. In small populations, scarce beneficial mutations are almost always eliminated." (ReMine p:220)

The Proof:

Rate of lethal mutations per gamete per generation = 1.5%

Occurrence of beneficial mutations = 1/1000 that of lethal

Rate of beneficial mutations per gamete per generation (v) = 1.5÷1000 % = 1.5x10^-5%

Selective advantage of beneficial mutations (s) = 0.01

Small population size (N) = 10,000

So, the number of substitutions per generation (K) = 4Nsv = 6x10^-3

Therefore the number of generations per substitution = 1/K = 167

The graph below shows that as the population gets smaller increasingly greater numbers of generations are needed for each gene substitution. eg 1,667 generations for a population of 1,000 individuals.

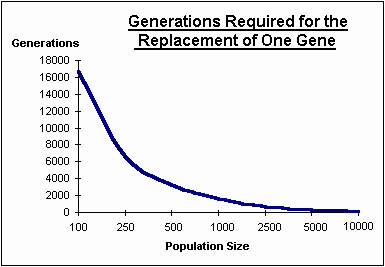
"Kimura and Ohta conclude that if the average selection value of beneficial mutations is one tenth percent (s=0.001) or less, then it is unlikely that K=1 [ie one substitution every generation] is attained unless the population size is a million or more. (ReMine footnote #20 p:221) (see M. Kimura & T. Ohta "Theoretical Aspects of Population Genetics", Princeton University Press, 1971)